Чурофметика ★
Слушатели Эха Москвы помнят недавнее интервью Чурова, в котором он опровергает математику:
Чуров совершенно правильно назвал свою аналогию с конфетками наперсточничеством. Я собираюсь показать это, предложив адекватную аналогию.
Статистический анализ результатов выборов никакого отношения к нескольким конфеткам не имеет. Чтобы правильно показать его суть, нужно представить следующую ситуацию.
Наш герой отправляется в каждый магазин известной торговой сети и покупает несколько упаковок
Известно, что в одну упаковку в силу ограниченности объема можно поместить не больше 100 конфет. Но так как конфеты до упора никто не набивает, разумно ожидать, что в среднем
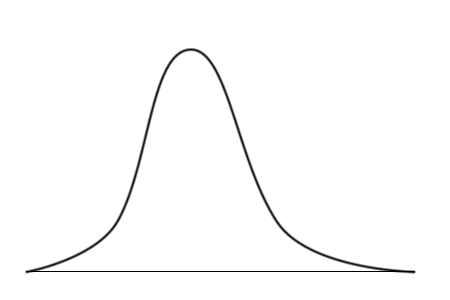
Как же удивляется исследователь, обнаружив нечто совершенно неожиданное!
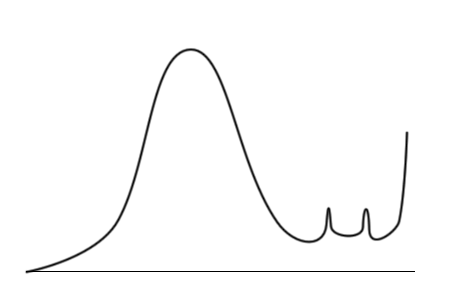
Здесь примечательны три вещи.
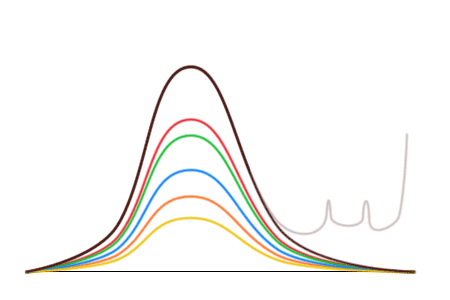
Тогда исследователь строит гистограммы, откладывая по вертикали не число упаковок, а уже общее число конфет разных цветов в упаковках с данным количеством конфет.
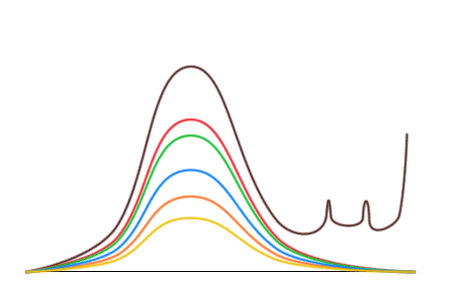
Оказывается, что безобразие действительно происходит только с коричневыми конфетами. Кривые для остальных конфет выглядят нормально и переходят друг в друга при растяжении или сжатии по вертикали. Их симметрия говорит о том, что конфеты ярких цветов в результате фальсификаций не изымаются. Таким образом, фальсификации заключаются только в преимущественном добавлении коричневых конфет.
Однако эти кривые позволяют сделать большее — сказать, сколько коричневых конфет было в упаковках до вброса! Так как левая половина коричневой кривой напоминает остальные, распределение которых не отличается от заводского, то можно растянуть красную кривую, чтобы левые половины красной и коричневой кривой совпали, и заменить искаженную правую часть.
«Это прекрасно, но какое отношение имеют все эти конфеты к выборам и причем здесь Чуров?» — спросит нетерпеливый читатель. Если заменить конфеты разных цветов на проценты за ту или иную партию, а упаковки
Подобный анализ проводился для выборов 2007 — 2009 годов и для последних думских выборов (идея несколько подробнее описана в первом материале). Анализ показывает, например, что на последних выборах Единая Россия получила не 49%, а 34%.
Вот такие, господин Чуров, конфетки!