видео
Чему же равно 6:2(1+2)?
Когда я впервые увидел этот пример в интернете, подумал, что это проблема на ровном месте. Да, мнения людей об ответе расходятся:
$${6\over 2(1+2)}={6\over 6}=1.$$
Борис Трушин смог снять по этой теме целых два видео по 18 минут:
После просмотра я сделал для себя такой вывод. Приоритет арифметических действий учат в начальной школе, а опускать знак умножения — только в средней школе. По характеру необходимых действий пример 6:2(1+2) — из начальной школы, поэтому он записан некорректно, умножение между двойкой и скобками опускать нельзя.
И совсем недавно мне попалось еще одно видео по теме. Оказывается, мнение о правильном ответе расходятся не только у спорящих в интернете, но и у производителей калькуляторов!
В этом видео отметил следующие вещи. Оказывается, около 100 лет назад еще были колебания в определении приоритета (явного) умножения и деления, но колебания приоритета неявного умножения над делением не было: если знак умножения опущен, выражение воспринимается единым целым, будто записано в скобках. К девяностым годам североамериканские учителя повлияли на производителей калькуляторов, чтобы те изменили приоритет неявного умножения и выровняли его с явным умножением и делением. Но так сделали не все производители, а сейчас происходит частичный откат к тому, что неявное произведение становится приоритетнее. Колебания приоритета неявного умножения относятся только обучению в школе, в профессиональном употреблении колебаний нет.
После просмотра этого видео я понял, что мой аргумент про использование двоеточия как знака деления в основном в начальной школе — это всего лишь отрицание проблемы. Действительно, использование горизонтальной черты для обозначения деления удобно в отдельных формулах, а не в сплошном тексте. Сейчас в математических текстах вместо двоеточия используется наклонная черта. Но никто не мешает спросить, чему равно
Я решил посмотреть, как сам записывал в одну строку формулы с делением и неявным умножением, и какие приоритеты подразумевал. Прошелся по текстам в блоге о теоретической физике старше нескольких лет, чтобы исключить возможное влияние обсуждений этого вирусного примера. В выражении
Раз уж мы обсуждаем приоритеты арифметических действий, поделюсь воспоминанием из начальной школы, кажется, из второго класса. Учительница нам говорила, что если в выражении на одном уровне несколько умножений и делений, то выполняются сначала деления, а потом умножения. Такого правила я больше нигде не встречал. Обычно учат, что умножение и деление выполняется подряд, слева направо. Например,
Срываем покровы
Я впервые увидел клип на песню Shocking blue — Venus (та самая «шизгара») 10 лет назад. Большим открытием стало, что ее поет не мужчина, а женщина. Я даже в твитер 9 января написал: «Всю жизнь думал, что песню Shocking blue — Venus поет мужик».
Сейчас случилось еще одно открытие такого же масштаба. Медуза написала о группе «Everything But The Girl». И я с удивлением узнал, что голос, поющий песню «Missing» — тоже не мужской, а женский!
Интересно, какое открытие ждет меня еще через 10 лет.
Как додуматься до решения олимпиадной задачи — 2
В прошлый раз я рассказывал о ходе своих мыслей при решении олимпиадной задачи. Может быть такие рассказы помогут
Условие задачи
Есть 3 различных натуральных числа $$x$$, $$y$$, $$z$$. Эти числа оказались подобраны так, что выражение
$$A={xy+yz+zx\over x+y+x}$$
тоже натуральное. Каким числом оно может быть? Иными словами, каково пересечение множества значений этой функции трех натуральных переменных и множества натуральных чисел?
Поиск решения
Идея №1: вынести в числителе за скобки $$xyz$$. Получается
$$A={\left({1\over x}+{1\over y}+{1\over z}\right)xyz\over x+y+x}.$$
Из этого я заметил, что при замене величин $$x$$, $$y$$ и $$z$$ на обратные $$1/x$$, $$1/y$$ и $$1/z$$ выражение «переворачивается», то есть $$A$$ меняется на $$1/A$$. Дальше у идеи не было очевидного развития, я решил попробовать другие идеи.
Идея №2: масштабирование. Видно, что если выполнить замену $$x$$, $$y$$ и $$z$$ на $$kx$$, $$ky$$ и $$kz$$, то числитель $$A$$ вырастет в $$k^2$$ раз, а знаменатель в $$k$$ раз, то есть $$A$$ меняется на $$kA$$. Как это можно применить? Пусть мы выбрали натуральные числа равными 1, 2 и 3. Тогда
$$A={2+6+3\over 1+2+3}={11\over 6}.$$
Чтобы из этого набора получить целое $$A=11$$, можно взять не 1, 2 и 3, а 6, 12 и 18.
Однако я не стал развивать дальше эту идею
Идея №3: перебор вариантов.
Чтобы прочувствовать задачу, часто бывает полезно рассмотреть некоторые частные случаи. В задачах вроде этой подобрать $$x$$, $$y$$ и $$z$$, чтобы выражение действительно было целым. В геометрических задачах бывает полезно нарисовать на черновике хороший чертеж, чтобы заметить закономерности вроде расположения точек на одной прямой или окружности.
Для перебора будем фиксировать значения $$x$$, $$y$$ и изменять $$z$$. Пусть $$x=y=1$$ (я проделал эту лишнюю работу, потому что невнимательно прочитал условие).
$$A={1+z+z\over 1+1+z}={1+2z\over 2+z}={4+2z-3\over 2+z}=2-{3\over 2+z}.$$
Ясно, что $$A=1$$ при $$z=1$$, а значение $$A=2$$ ни при каком $$z$$ не будет достигнуто.
Пусть $$x=1, y=2$$. Тогда
$$A={2+2z+z\over 1+2+z}={2+3z\over 3+z}.$$
Если $$z$$ нечетное, то числитель нечетный, знаменатель четный, $$A$$ не будет целым. Если $$z$$ четное, то числитель четный, знаменатель нечетный. Здесь я сделал еще одну ошибку, подумав, что четное число не может делиться на нечетное, и вообще исключил из рассмотрения варианты с $$x$$ и $$y$$ разной четности.
Пусть $$x=1, y=3$$. Тогда
$$A={3+3z+z\over 1+3+z}={3+4z\over 4+z}.$$
Здесь исключаем случай четного $$z$$, так как нечетный знаменатель не будет делиться на четный числитель. Попробуем подставить разные нечетные $$z$$. Получим:
$$ z=1\implies A={7/5}\\ z=3\implies A={12/7}\\ z=5\implies A={23/9}\\ z=7\implies A={31/11}\\ z=9\implies A={39/13}=3\\ z=11\implies A={47/15}\\ $$
Далее, сколько бы мы ни увеличивали $$z$$, до значения 4 мы не дойдем, так как 4 достигается только в пределе $$z\to\infty$$. Таким образом, при $$x=1, y=3$$ единственное целое $$A$$ дает $$z=9$$.
Пусть $$x=1, y=5$$. Тогда
$$A={5+5z+z\over 1+5+z}={5+6z\over 6+z}.$$
Перебор $$z$$ слишком долгий, и мы понимаем, что возможных значений $$A$$ не так уж много. Поэтому решим уравнение относительно $$z$$:
$$5+6z=A(6+z)\iff(6-A)z=6A-5\implies z={6A-5\over 6-A}.$$
Отсюда видно, что $$A$$ не может быть четным. 1 и 3 не подходят, $$A=5$$ дает $$z=25$$, других значений для проверки нет.
Мы видим, что значения переменных (1, 3, 9) и (1, 5, 25) дают целые значения $$A$$. Кажется, это и есть нужная закономерность.
Решение
Подставим значения $$x=1, y=n, z=n^2$$. Тогда
$$A={n+n^3+n^2\over 1+n+n^2}=n\,{1+n^2+n\over 1+n+n^2}=n.$$
Таким образом, мы можем в качестве значения выражения получить любое натуральное число, не равное 1. То, что 1 получить нельзя, посмотрите у Савватеева или докажите самостоятельно.
Обсуждение ошибок
После подстановки $$x=1, y=n, z=n^2$$ моя ошибка с четностью стала очевидной. Сначала мне вообще не хотелось писать об ошибках. Признаваться в них не очень приятно. Но с другой стороны, благодаря ошибкам на этапе поиска решения я довольно быстро нашел правильное решение. Могло бы оказаться так, что я углубился в разработку
Чтобы минимизировать ошибки на олимпиадах, важно не переписывать решение с черновика на чистовик, а заново решить задачу на чистовике, обращаясь к черновику только для сравнения вычислений. Об этом и других советах я уже писал в руководстве олимпиадника.
Поиграл на рояле в аэропорту
Как просили в прошлый раз в комментариях, снял на видео, как поиграл в аэропорту. Не без ошибок, потому что клавиатура непривычная: черные клавиши оказались слишком тонкие. Да и месяц не садился за инструмент. Вот несколько фрагментов:
0:00 Разминка
1:20 Chilly Gonzales — Dot
1:51 Roman Parpalak — Ursa Minor
3:39 Ludovico Einaudi — Nightbook
5:22 Chilly Gonzales — Gogol
6:25 Secret Garden — Song from a Secret Garden
Как додуматься до решения олимпиадной задачи?
Я иногда решаю «для себя»
Вчера решил очередную такую задачу из ролика Савватеева. Честно остановил ролик перед решением, задумался и нашел решение. Расскажу скорее не о самом решении, а о том, как можно его отыскать.
Условие задачи
В задаче требуется показать, что существует действительное число $$A\in\R$$, такое что любая натуральная степень $$n$$ этого числа после округления вверх отличается по модулю от ближайшего квадрата натурального числа ровно на 2.
Анализ условия
Запишем условие задачи формально: требуется доказать, что
$$\exists A\in\R\ \forall n\in\mathbb{N}\ \exists x\in\mathbb{N}:\left|\lceil A^n\rceil-x^2\right|=2.$$(1)
Здесь потерялось условие, что число $$x^2$$ должно быть ближайшим квадратом к $$\lceil A^n\rceil$$. Но оно будет выполнено автоматически, если $$A>5$$.
Условие выглядит страшно, и непонятно, как подступиться к задаче. В математике нет стандартных приемов по работе с округлением вверх. Придется пользоваться универсальным приемом: думать.
Перепишем условие менее формально. Для каждого $$n$$ должны найтись числа $$\varepsilon\in[0,1)$$ и $$x^2$$, для которых $$A^n+\varepsilon=x^2\pm2$$. При больших $$n$$ получаем, что $$A^n\approx x^2$$.
Озарение
Теперь самое время для озарения. Оно пришло ко мне в ходе такого рассуждения. Переход от $$n$$ к $$n+1$$ в левой части сводится к домножению на $$A$$, а в правой части — к переходу от одного квадрата к другому.
Квадраты натуральных чисел расположены по определенному шаблону. Разница между соседними квадратами — это последовательность нечетных чисел. Скорее всего в правой части при переходе от одного квадрата к другому прибавляется некоторое число, возможно связанное с $$A$$.
Вспоминаем, в каком случае домножение сводится к прибавлению? Есть известный пример для золотого сечения и для рекуррентных последовательностей типа Фибоначчи. Золотое сечение $$\varphi=(1+\sqrt5)/2$$ обладает свойством $$\varphi^{n+1}=\varphi^n+\varphi^{n-1}$$. То есть домножение $$\varphi^n$$ на $$\varphi$$ эквивалентно прибавлению $$\varphi^{n-1}$$. Возможно, число $$A$$
Гипотеза
Проверим гипотезу, что золотое сечение подходит на роль числа $$A$$. Вычислим для начальных $$n$$ степени золотого сечения и посмотрим, есть ли у них квадрат, отличающийся почти на 2:
| $$n$$ | $$\varphi^n$$ | Квадрат |
| 0 | 1 | |
| 1 | 1,618034 | |
| 2 | 2,618034 | |
| 3 | 4,236068 | |
| 4 | 6,854102 | 9 |
| 5 | 11,090170 | |
| 6 | 17,944272 | 16 |
| 7 | 29,034442 | |
| 8 | 46,978714 | 49 |
| 9 | 76,013156 | |
| 10 | 122,991869 | 121 |
| 11 | 199,005025 | |
| 12 | 321,996894 | 324 |
| 13 | 521,001919 | |
| 14 | 842,998814 | 841 |
| 15 | 1364,000733 | |
| 16 | 2206,999547 | 2209 |
Для малых $$n$$ закономерности не видно. Но начиная с $$n=4$$ у каждого второго числа находится нужный квадрат! Наше вычисление показывает, что $$\varphi^2=2,\!618034$$ — неплохой кандидат для числа $$A$$. Оно подошло бы под условие, если бы не требование того, что именно ближайший квадрат, а не некоторый, должен отличаться на 2. Действительно, $$\varphi^2$$, округленное вверх до 3, отличается от квадрата 12 на 2. Чтобы учесть это требование, можем отобрать из таблицы не каждое второе число, а каждое четвертое, и положить $$A=\varphi^4$$.
Поскольку речь зашла о золотом сечении и числах Фибоначчи, мы можем понять, откуда в условии взялось округление вверх. Известно, что для чисел Фибоначчи $$F_{n}$$ есть формула Бине:
$$F_{n}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}}.$$
Для нашей задачи от нее толку мало, но она подсказывает, что мы можем добавить к иррациональному $$\varphi^n$$
Строгое доказательство
Докажем теперь, что $$\varphi^{2n}+\varphi^{-2n}$$ отличается от квадрата некоторого натурального числа на 2. Для этого рассмотрим вспомогательное число $$t_n=\varphi^{n}+(-\varphi)^{-n}$$.
Заметим, что $$(-\varphi)^{-1}=-2/(1+\sqrt{5})=(1-\sqrt{5})/2$$, как и $$\varphi$$, является решением уравнения $$y^{2}=y+1$$ и, следовательно, тоже удовлетворяет условию $$y^{n+1}=y^n+y^{n-1}$$. Итого имеем рекуррентную последовательность $$t_n=\varphi^{n}+(-\varphi)^{-n}$$, подчиняющуюся определению $$t_{n+1}=t_n+t_{n-1}$$, так как она есть сумма двух других рекуррентных последовательностей с тем же определением.
Вычислим начальные элементы последовательности $$t_n$$: $$t_0=1+1=2$$, $$t_1=(1+\sqrt{5})/2+(1-\sqrt{5})/2=1$$. По принципу математической индукции любой элемент последовательности $$t_n$$ — также целое число.
Возведем элемент последовательности $$t_n$$ в квадрат:
$$t^2_n=\left(\varphi^{n}+\left({-1\over\varphi}\right)^n\right)^2=\varphi^{2n}+{1\over\varphi^{2n}}+2(-1)^n.$$(2)
Таким образом, возведение $$\varphi^2$$ в степень $$n$$ и округление вверх дает целое число $$\varphi^{2n}+1/{\varphi^{2n}}$$, отличающееся от квадрата натурального числа $$|t_n|=|\varphi^{n}+(-\varphi)^{-n}|$$ ровно на 2.
Сравнение решения с авторским
Мое решение вроде бы завязано на золотое сечение и на его свойства. Но на самом деле используется только одно свойство: золотое сечение есть решение уравнения $$y^{2}=y+1$$. Сумма степеней корней этого уравнения порождает целочисленную последовательность. Есть и другие уравнения с тем же свойством. Корни по модулю должны быть взаимно обратными, чтобы сработало равенство наподобие (2). Можно было взять действительные корни любого уравнения $$y^{2}=ky\pm1$$ с целым $$k\neq\pm2$$.
Савватеев использовал свойства симметрических многочленов, чтобы показать целочисленность суммы степеней корней. Мой способ через математическую индукцию и рекуррентные последовательности тоже годится.
Анализ данных — В кресле препода №7
За последние несколько месяцев было крупных новостей, связанных с анализом данных. Мне как физику такие новости интересны и понятны, потому что современную физику нельзя представить без анализа данных. В очередном выпуске «В кресле препода» объясняю на конкретных примерах, как работает анализ и представление данных.
00:00 Резонансные новости, связанные с анализом данных
01:03 Анализ данных пришел из физики высоких энергий
02:25 Обработка данных с Большого адронного коллайдера
03:30 Настоящая Big Data на Большом адронном коллайдере: в «гриде» LHC идет запись 300 мегабайт данных в секунду
05:03 Визуализация и анализ данных на примере графика заболеваемости коронавирусом Яндекса
12:40 Как понять истинный масштаб заражений коронавирусом в России по избыточной смертности
19:38 Как распознать фальсификации на голосовании
29:39 Расследование Грозева об отравлении Навального
32:27 Анализ данных как современный научный метод против средневековой пропаганды
Связь между физикой и программированием: абстракции и язык — В кресле препода №6
Я заметил нетривиальную связь между физикой и программированием. Она находится в области используемых и там и там абстракций и обозначений. Записал видео с объяснением и примерами.
Придумал название «В кресле препода» для таких видео, где я обсуждаю
00:00:47 Зачем слушать этот рассказ
00:01:33 Замечание о формате презентаций
00:03:15 План рассказа
00:04:01 Математический аппарат физических теорий
00:05:39 Механика Ньютона и двойной маятник
00:09:45 Уравнения Максвелла: векторная и компонентная форма записи
00:14:17 Четырехвекторы и скорость света
00:18:01 Принцип наименьшего действия
00:21:25 Разнообразие форм уравнений Максвелла
00:23:41 Причем здесь программирование?
00:28:28 Уровни абстракций в языках программирования: физический, процедурный, ООП
00:33:26 Кто создает больше абстракций: физик или программист?
00:37:23 Практический пример
00:41:21 Разбор примера обработки
00:48:50 Переписывание примера из документации в объектном стиле и добавление функциональности на примере головоломки Арнольда (исходник на гитхабе)
01:17:58 О «пользе» MVC и что такое ООП на самом деле
01:20:35 Сравнение процедурного и объектного подходов и принцип High Cohesion Low Couping
01:23:42 Наследования и полиморфизма нет, а дух ООП есть
Описание головоломки Арнольда в предыдущем посте и на хабре.
Понятие формата в дизайне интерфейсов — В кресле препода №5
Когда формулировал, почему моим словам стоит доверять, осознал, что у меня уже почти 13 лет опыта в коммерческой
00:11 Почему моим словам стоит доверять: 13 лет опыта
00:42 Собирался рассказать о понятии формата давно
01:11 Для затравки: чем плохи выпадайки в вебе, пример личного кабинета
03:28 Понятие формата
04:56 Пример 1: формат веба и формат окон настройки старых операционных систем (сравнение из старой статьи на хабре)
08:03 Комментарий к статье, обращающийся к понятию формата
10:42 OS/2 умер
12:09 Окно настройки — почему такое? Ограничение 1: физический размер экранов
14:24 Ограничение 2: размер видеопамяти
15:26 Ограничение 3: частота обновления
18:53 Ограничение 4: работа без драйверов
19:54 640*480 — естественное ограничение в конце
20:58 Особенности формата веба
22:47 Сравнивать надо функциональность
25:28 Бессмысленность претензий к вебу
26:52 Эволюция интерфейса настройки Windows
32:28 Пример 2: Одностраничные приложения
33:54 Админка моего движка как пример одностраничного приложения
37:25 Как бы сейчас спроектировал интерфейс админки
41:42 Обсуждаем извлеченные уроки и дизайн выпадайки из личного кабинета
46:17 Итог
Уборка улиц, отрицательная польза и коррупция
Выглянул в окно и увидел, как дворник заметает мусор под припаркованные машины. Сходил за мобильником и начал снимать. Он перестал сметать мусор под машины, но стал — на газон. После фотографировал чистый асфальт. А под конец перекинул мешок с мусором через ограждение вырытой ямы, хотя до мусорных баков было метров 10.
Смысла от его действий нет никакого. Ветер сдует и дождь смоет грязь опять на асфальт. Результат работы дворника — не чистый двор, а фотографии чистого асфальта. Он продает эти фотографии, а управляющая компания их покупает.
Понятно, почему такое происходит. Вместо того чтобы купить уличный пылесос и нанять оператора за нормальную зарплату, нанимается низкоквалифицированная рабочая сила, а остальные деньги разворовываются.
Латынина об этом говорила не один раз:
У нас до сих пор через железнодорожные переезды вокруг Москвы не построены нормальные автомобильные переезды, у нас автомобили стоят в пробке по несколько часов. При этом рядом как всегда таджики косят траву, нанятые, видимо, Железной дорогой.
То есть вот это вот… Извините, что я постоянно возвращаюсь к этим косящим траву таджикам. Но это такое абсолютно зримое воплощение принципа о том, что если вы хотите украсть, то чем более бесполезна работа, которую выполняют люди, тем больше вы можете украсть. Потому что, ну, понятно: если таджики косят траву, то на этом украсть можно больше, чем если даже те же таджики (я уж не говорю о том, чтобы русские рабочие) построили переезд через эту несчастную железную дорогу.
О тестовых заданиях на собеседованиях программистов — В кресле препода №4
Я провел много собеседований. Несколько десятков, или даже около сотни. К сожалению, с самого начала подсчитывать не догадался. Точное число было бы интересным.
Сейчас в очередной раз ищу сильного разработчика (если меня читают такие — напишите). Просматривал резюме и остановился на одном, в котором кандидат написал, что не выполняет тестовые задания бесплатно. В видео ниже я рассказал о том, как открыл его гитхаб, какие выводы сделал, какое тестовое задание выдаю я сам и с какой целью.
Кстати, видео снимал по методу Ильи Бирмана.
Одновременная вставка уникальных значений в словарные таблицы — В кресле препода №3
Как правильно добавлять данные в словарную таблицу с уникальными строками одновременно из нескольких потоков? В PostgreSQL вот так:
CREATE TABLE words (
id SERIAL PRIMARY KEY,
word TEXT NOT NULL UNIQUE
);
BEGIN;
SELECT id FROM words WHERE word = 'a';
INSERT IGNORE INTO words (word) VALUES ('a');
SELECT id FROM words WHERE word = 'a';
COMMIT;В видео рассказываю, почему именно так, и показываю, как это работает.
00:25 Пример
01:34 Демонстрация наивной реализации вставки в словарные таблицы
02:32 Недостаток: появление дублей
03:45 Демонстрация уникального индекса
04:47 Недостаток одного только уникального индекса
05:55 Нет поддержки целостности ⇒ нужны транзакции
06:37 Демонстрация параллельной вставки в таблицу с уникальным индексом в транзакции
08:59 Вставка с игнорированием
09:17 Демонстрация вставки с игнорированием в транзакции с уровнем READ COMMITTED
12:15 Демонстрация дедлока при вставке с игнорированием в транзакции с уровнем REPEATABLE READ
13:44 Особенности метода в MySQL
Видео Ирумы
Ирума — один из трех моих любимых композиторов. Я дважды был на его концертах. К сожалению, в интернете мало видеозаписей его игры в хорошем качестве. С удовольствием посмотрел недавно появившуюся запись, где он играет свои самые известные композиции.
Лекция Казакова
Центр Архэ молодцы, выкладывают много интересных видео. Например, лекция с Дмитрием Казаковым об ожидаемых открытиях в физике элементарных частиц разбавит уже надоевший коронавирус.
Посмотрел с теплыми воспоминаниями.
За 7 лет мало что изменилось: кроме бозона Хиггса на LHC пока ничего не открыли, продолжат эксперименты до 2035 года; денег на новые ускорители нет; надежда не на рост энергий, а на повышение точности; темная материя не открыта; развитие астрофизики многообещающее.
Задача о взвешенном выборе и случайной величине — В кресле препода №2
Объясняю на
Пусть заданы n положительных чисел $$w_1$$, $$w_2$$, … $$w_n$$. Для каждого из них выберем значение $$x_i$$ случайной величины, равномерно распределенной на единичном интервале (0, 1). Существует ли функция $$f_w(x)$$, такая что максимальное значение этой функции $$\inline\max_{i=1,2,...n}\left\{f_{w_i}(x_i)\right\}$$ достигается на k-той выбранной паре $$(w_k, x_k)$$ с вероятностью, пропорциональной $$w_k$$?
Вместо более чем часового видео можете сразу прочитать решение без лишней воды.
Слушают и задают вопросы: Максим Федоров, Руслан Яруллин, Роман Попов, Михаил Чернявский.
Инструменты: Zoom, Sony Vegas Pro, Audacity, наушники Logitech, планшет Asus, самодельный стилус из предыдущего видео.
Как сделать стилус для планшета
Сделал себе стилус для планшета, засняв процесс на видео. Если интересен только результат, мотайте ролик в конец.
Картинку из поста про касания лица нарисовал похожим стилусом.
Звук вышел не очень. Отдельного микрофона у меня нет, писал на встроенный в камеру. И автоматический баланс белого пляшет, надо было фиксированный выбрать.
Дезинфекция во время эпидемии
Рабочие опрыскивают непонятным пенистым раствором двор, детские площадки, подъезды.
Зачем это нужно, если коронавирус живет на поверхностях несколько часов? Это же не радиация? Кстати, сходство с сериалом «Чернобыль» оцените самостоятельно:

Фортепиано ★
Позавчера улетел из Кишинева. В зале вылета опять поставили рояль. Не очень хотелось кому попало давать мобильник для съемки ролика. Вместо этого записал игру на своем инструменте. Это хорошо известная композиция:
А это новая композиция. С помарками, но зато сейчас, а не еще через три года:
Популярные песни сегодня и 20 лет назад
Рик Беато сделал два микса из 20 песен, популярных сегодня и в 1998 году.
Конечно, я буду говорить как старпер, что сегодня в моде помидоры вкуснее солнце ярче. Но даже непредвзятое сравнение показывает, что популярная музыка конца девяностых была разнообразнее и мелодичнее.
Экспонента
Смотрю лекции Алексея Савватеева по математике и получаю удовольствие. Вот лекция, в которой он переделал вузовский курс математики так, что его половина связана с изучением разных свойств экспоненты:
С 1:15:20 он строго доказывает формулу Эйлера о мнимой экспоненте $$e^{iy}=\sin y+i\cos y$$ тем же нестандартным методом, который я использовал в своей заметке про экспоненту и приближенные методы.
Пишем объектно-ориентированный код в PhpStorm — В кресле препода №1
В прошлом посте я разрушал мифы о среде разработки PhpStorm. В продолжение я записал скринкаст о том, как в ней писать
Скринкаст рассчитан на людей, не владеющих уверенно ООП. На записи я перевожу фрагмент кода из процедурного стиля в
Содержание:
00:19 Процедурный стиль vs.
01:11 PHP не для процедурного программирования
02:22 ООП в PHP: много рутины
03:05 Задача: показать не только приемы работы в PhpStorm, но и пользу от ООП
04:08 Выбираем код для рефакторинга
05:10 Создаем класс: пространство имен; методы; константы
10:36 Автозагрузка классов через composer
13:28 Разбираем проблемы кода
15:34 Возвращаем вместо массива объект (DTO)
24:29 Избавляемся от глобальных переменных по принципу инверсии зависимостей (dependency inversion)
29:29 Наполняем DTO логикой: __toString
33:16 Рефакторинг
35:14 Наполняем DTO логикой: валидация в конструкторе
39:40 Получился код по принципам SOLID
40:24 Проблема создания сервисов
41:04 Решение с помощью контейнеров зависимостей; подключение Pimple через composer
46:01 Обзор изменений, привнесенных
48:09 Дополнение: подключаем библиотеку поиска Rose, описывая сервисы в контейнере
01:01:38 Подведение итогов
Прогулка против коррупции
— Уважаемые граждане! Проходим все вниз. Площадь Пушкина переполнена.
— Переполнена полицейскими!
С Новым годом!
Под Новый год принято подводить итоги года уходящего. А я хочу вспомнить о событиях двенадцатилетней давности. Тогда на международной олимпиаде по физике мы обсуждали, что в Молдавии олимпиада будет проходить в 2017 году. Страна станет нормальной и достойно проведет олимпиаду. Но так не случилось. Власть передала (или продала?) это право Индонезии, и олимпиада будет на Бали.
Тогда казалось, что впереди много времени, и столько всего случится. Хоть я поступал учиться на физика, я выбирал между физикой и информатикой. Поэтому мало удивительного в том, что сейчас я зарабатываю программированием. Удивительно другое: за это время я заинтересовался и увлекся музыкой.
2004 год, поездка на вступительные экзамены, общежитие ФОПФ МФТИ:

Музыкальное поздравление с 2017 годом:
Сочиняем музыку по первой фразе
Хочу написать серию постов о сочинении музыки и на примере своих композиций показать, что это не такое сложное занятие. Начнем с создания музыки по первой фразе.
Если вы пробовали сочинять стихи, то знаете, что с первой строчкой дело упрощается. Действительно, первая строчка задает тему. Чередование ударных и безударных слогов определяет размер стихотворения. Последнее слово рифмуется. Эти ограничения
При сочинении музыки можно использовать такой же прием. Логика развития музыки и гармонические отношения между звуками разворачивают начальный набор звуков в полное произведение. Я расскажу об этом приеме на примере своей композиции, черновую версию которой записал на видео. Название пока не придумал, поделитесь в комментариях идеями.
Основа композиции
Выбираем тональность. Я опустил расслабленные руки на клавиатуру. В левой оказалась октава до, в правой — октава ми. Это неполный
Добавляем ритм. Левая рука играет октавы через равные промежутки времени. Правая начинает вместе с левой, но затем отстает, и звуки до и ми начинают чередоваться. Такова наша первая фраза.
Добавляем движение. Левая рука постепенно спускается по звукам тональности
Определяемся с последовательностью аккордов. Продолжаем спуск и получаем C, Bm, Am, G, F, Em, Dm, E, Am/C. Обратите внимание на последние три аккорда. В предпоследнем бас повернул назад, в ми. Это нужно, чтобы сыграть основную формулу гармонии Dm — E — Am и перейти в параллельную тональность ля минор.
Добавляем мелодию. Сейчас правая рука играет звуки текущей гармонии, задерживаясь при ее смене. Это слишком скучно. Разрешим голосу правой руки отклоняться от этой схемы:
Форма
Первая часть готова. Она начинается в до мажоре и заканчивается в ля миноре. Звуки этих аккордов между собой сочетаются, так что после первой части повторяем ее же с другим аккомпанементом. Мелодия первой части сама по себе разнообразна, и я решил обойтись без вариаций. Повторять эту часть по кругу больше нельзя. Придумаем другие части.
Мелодическая пауза. Первая часть заканчивается в тональности ля минор, так что заполняю паузу звуками аккорда ля минор. Следуя приему первой части спускаюсь по ступеням: Аm, G, F, E. Повторяю первую часть.
Вторая часть. Чтобы повторить первую часть еще раз, опять переходим из ля минора в до мажор. Возьмем первые четыре аккорда золотой секвенции (Am, Dm, G, C) и поддержим простой мелодией.
Итоговая форма:
Часть 1* — часть 1 — мелодическая пауза — часть 1 — часть 2 — часть 1
Может быть, вместо слабой второй части я сочиню другой фрагмент, и композиция окончательно оформится.
В следующий раз поговорим о сочинении музыки к стихотворениям.
Какую Вселенную видит фотон?
Помните известный ролик «от Солнца до Юпитера за 44 минуты»?
Я написал о том, что бы увидел фотон, если не игнорировать теорию относительности.
Марш мира
На этот раз пробую формат видеоотчета.
Народу было много, примерно как в прошлый раз. Заявленное число в 26 тысяч похоже на правду.
Вертолет
Не каждый день за окном увидишь вертолет.
Видео о движке сайтов S2
Сделал видео о своем движке сайтов S2:
В хорошем качестве смотрите на главной сайта движка.
Народные гулянья на Чистых прудах
Сегодня я был в центре Москвы и пришел к Чистым прудам. В шесть вечера там проходил
К памятнику «непонятному казаху» Абаю Кунанбаеву я вернулся около девяти. Концерт уже закончился.

Собчак и Яшин

А вот протестующий повесил на себя и белую ленту, и георгиевскую, и триколор. Видимо, для надежности.

Революционная накидка.

Потом народ стал массово петь.
Проезжающие машины поддерживают гулянья.
Люди стоят рядом небольшими группами,
Подъезжающие автобусы с полицией бурно приветствовались криками «Еще, еще!». Впрочем, при мне полиция активных действий не проявляла.
За этими народными гуляньями забавнее наблюдать в онлайновой трансляции. Когда присутствуешь на месте событий, складывается впечатление, что там собрались люди, которым нечем заняться (хотя это и не так; я уважаю тех, кто остается на ночь). На месте власти я бы их игнорировал, и они бы сами собой разошлись. Но необъяснимые действия власти способны только раззадорить. И арест Навального и Удальцова эти акции не прекратит. Власть сама выращивает лидера оппозиции.
Чурофметика ★
Слушатели Эха Москвы помнят недавнее интервью Чурова, в котором он опровергает математику:
Чуров совершенно правильно назвал свою аналогию с конфетками наперсточничеством. Я собираюсь показать это, предложив адекватную аналогию.
Статистический анализ результатов выборов никакого отношения к нескольким конфеткам не имеет. Чтобы правильно показать его суть, нужно представить следующую ситуацию.
Наш герой отправляется в каждый магазин известной торговой сети и покупает несколько упаковок
Известно, что в одну упаковку в силу ограниченности объема можно поместить не больше 100 конфет. Но так как конфеты до упора никто не набивает, разумно ожидать, что в среднем
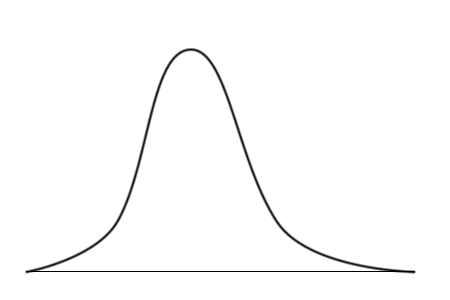
Как же удивляется исследователь, обнаружив нечто совершенно неожиданное!
Здесь примечательны три вещи.
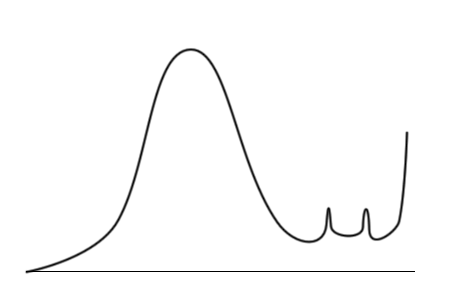
Тогда исследователь строит гистограммы, откладывая по вертикали не число упаковок, а уже общее число конфет разных цветов в упаковках с данным количеством конфет.
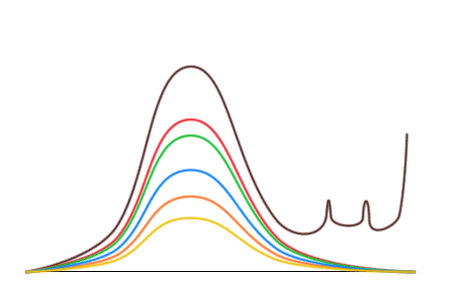
Оказывается, что безобразие действительно происходит только с коричневыми конфетами. Кривые для остальных конфет выглядят нормально и переходят друг в друга при растяжении или сжатии по вертикали. Их симметрия говорит о том, что конфеты ярких цветов в результате фальсификаций не изымаются. Таким образом, фальсификации заключаются только в преимущественном добавлении коричневых конфет.
Однако эти кривые позволяют сделать большее — сказать, сколько коричневых конфет было в упаковках до вброса! Так как левая половина коричневой кривой напоминает остальные, распределение которых не отличается от заводского, то можно растянуть красную кривую, чтобы левые половины красной и коричневой кривой совпали, и заменить искаженную правую часть.
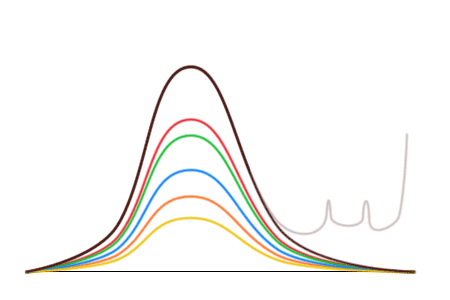
«Это прекрасно, но какое отношение имеют все эти конфеты к выборам и причем здесь Чуров?» — спросит нетерпеливый читатель. Если заменить конфеты разных цветов на проценты за ту или иную партию, а упаковки
Подобный анализ проводился для выборов 2007 — 2009 годов и для последних думских выборов (идея несколько подробнее описана в первом материале). Анализ показывает, например, что на последних выборах Единая Россия получила не 49%, а 34%.
Вот такие, господин Чуров, конфетки!