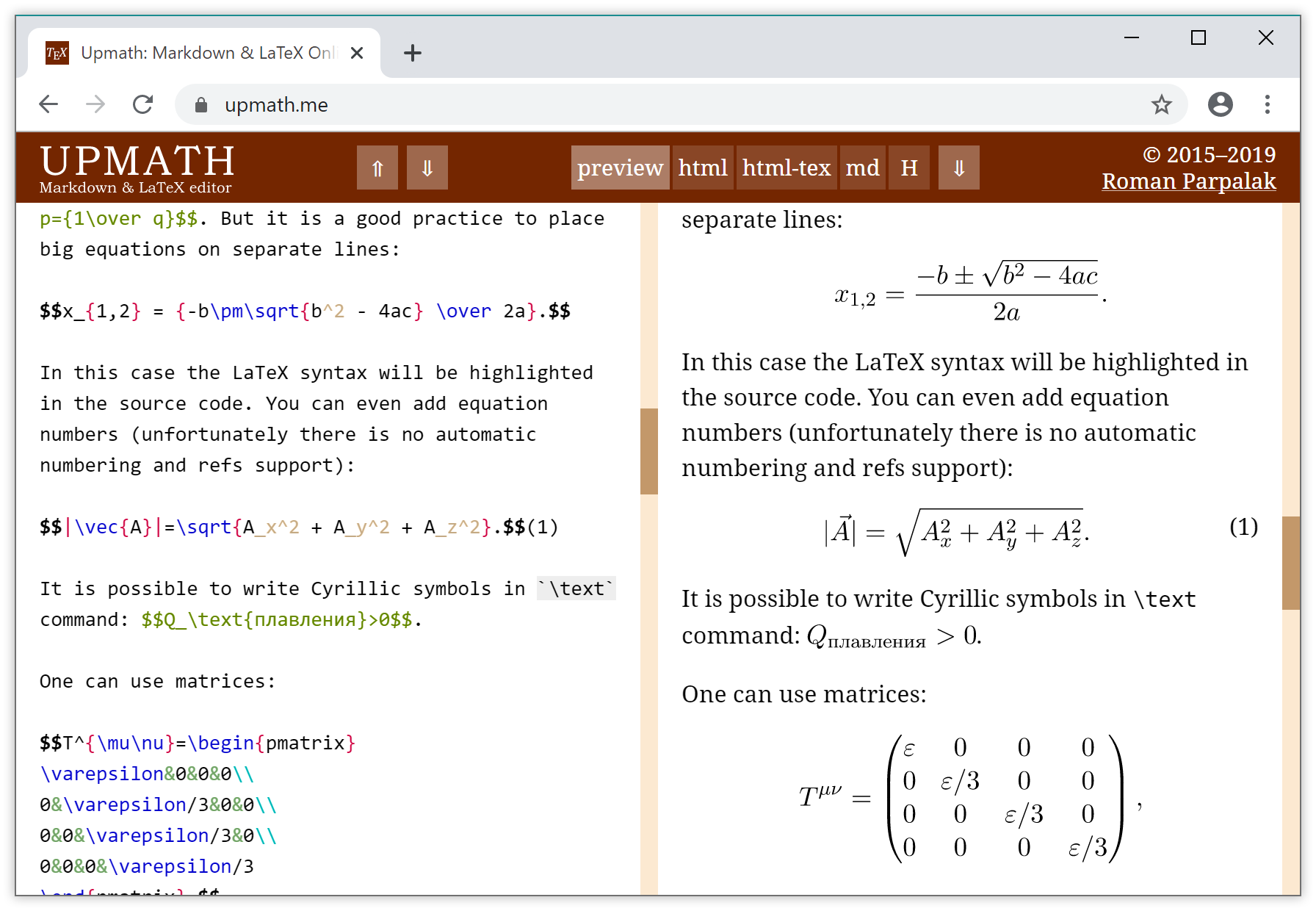
upmath
Upmath — это редактор математических текстов для интернета. Оформляете текст в маркдауне, пишете формулы на латехе, а Upmath выдает
Статьи по этой теме:
Латех и
RSS, формулы и Feedly
Постоянные читатели помнят, что у меня есть сервис по превращению математических формул в картинки и редактор для создания математических текстов. С заменой формул на картинки на обычных
Еще в 2011 году я стал отдавать в RSS растровые картинки, потому что непонятно, в каком окружении будет отображаться контент оттуда. А на обычных
Когда в 2013 году прекратила работать
У Feedly была одна особенность с отображением картинок: они принудительно становились плавающими (включалось
Сейчас я решил проверить, не научился ли Feedly отображать нормально картинки. Оказалось, что научился. Если вы читаете этот текст через RSS в Feedly, можете в этом убедиться в предыдущем абзаце.
Чтобы два раза не вставать, я попросил ChatGPT составить
<?xml version="1.0" encoding="UTF-8"?>
<xsl:stylesheet version="1.0" xmlns:xsl="http://www.w3.org/1999/XSL/Transform">
<xsl:template match="/">
<html>
<head>
<title><xsl:value-of select="rss/channel/title" /></title>
<style type="text/css">
a {
color: #56d;
text-decoration-thickness: 1px;
text-decoration-color: rgba(85, 102, 221, 0.5);
}
body {
max-width: 720px;
font: 16px/1.5 sans-serif;
margin: 0 auto;
}
h1, h2, h3 {
margin: 1em 0 0.25em;
}
p {
margin: 0 0 0.75em;
}
</style>
</head>
<body>
<h1>
<a href="{rss/channel/link}">
<xsl:value-of select="rss/channel/title" />
</a>
</h1>
<xsl:for-each select="rss/channel/item">
<div class="item">
<h2><a href="{link}"><xsl:value-of select="title" /></a></h2>
<div><xsl:value-of select="description" disable-output-escaping="yes" /></div>
</div>
</xsl:for-each>
</body>
</html>
</xsl:template>
</xsl:stylesheet>
Чтобы это заработало, нужно добавить ссылку на такой
<?xml version="1.0" encoding="utf-8"?>
<?xml-stylesheet href="/_styles/rss.xslt" type="text/xsl"?>
<rss version="2.0">
<channel>
...
</channel>
</rss>
Кстати, пока со всем этим возился, обнаружил, что в RSS сломалось отображение исходного кода: перестало работать сохранение переносов строк внутри тегов <pre><code>. Долго пытался понять, где ошибка, пока не осознал, что это сломался сам Feedly. Похоже, эта проблема наблюдается в любых источниках в Feedly за последние недели две. Заодно сейчас и проверим, нормально ли будет отформатирован код в этой заметке.
В заключение полезный совет: если хотите отладить RSS и не хотите ждать, пока Feedly проиндексирует новую запись, можете на экране добавления нового источника добавить в URL не меняющую смысла часть запроса. Тогда Feedly распарсит RSS на лету и отобразит три последних записи:
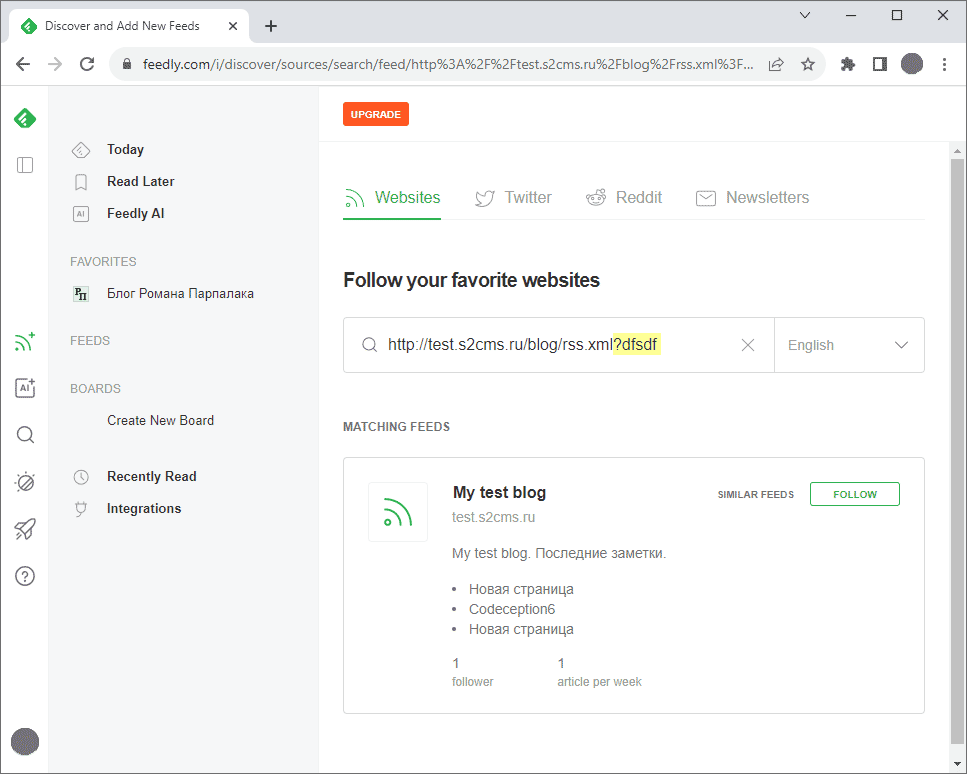
Добавлено позднее: оказывается, Feedly нормально отображает картинки только в
Воспринимайте слова в переписке буквально
В общении между людьми есть проблема недопонимания. Говорящий не всегда правильно подбирает слова, а слушающий додумывает. Иногда получается, что имели в виду одно, сказали другое, а поняли третье.
В устном общении есть возможность задать уточняющий вопрос, и проблема часто снимается. В переписке с этим сложнее, поэтому особенно важно следить за словами: проверять, правильно ли слова передают смысл, и воспринимать слова буквально.
Смотрите, что получается, если
Во всех адресах и примерах использования «https:»почему-то исчезло. Так что адреса формально неправильные.
Чтобы не отправлять вас по ссылкам, поясню, что сервис предлагает УРЛы картинок в виде //i.upmath.me/svg/f(x) и код встраивания скрипта <script src="//i.upmath.me/latex.js"></script>.
Дело в том, что схема (http или https для веба) — необязательная часть адреса, его можно опустить (см.
Посетитель вложил в свою мысль целых два неверных утверждения. Первое: https
Если бы посетитель спросил, почему так сделано, я бы ответил, и может быть даже погуглил за него. Но вопроса не было, поэтому в своем ответе я задал уточняющие вопросы:
Это вопрос или предложение? Почему вы считаете, что «https:» исчезло?
Первая часть — отсылка к технике продуктивной переписки «общаться вопросами и предложениями». Непонятно, интересовался ли посетитель, почему так сделано, или предлагал сделать
Закрепим рекомендации:
- Когда вы пишете сообщение в мессенджере или почте, перечитайте перед отправкой и проверьте, что сообщение отражает вашу мысль.
- Когда вы получили сообщение, воспринимайте его буквально, не додумывайте за автора. Если автору нужно было другое, он переспросит.
- Отвечайте на явно сформулированные вопросы. Прокомментируйте предложения: будем ли мы делать то, что предлагается, и если нет, то почему.
- Если ни вопросов, ни предложений нет, а от вас требуется реакция, и вы не знаете, что ответить, так и напишите: «Я не понимаю, в чем твой вопрос и что ты предлагаешь».
Редактор математических текстов Mathcha
Искал
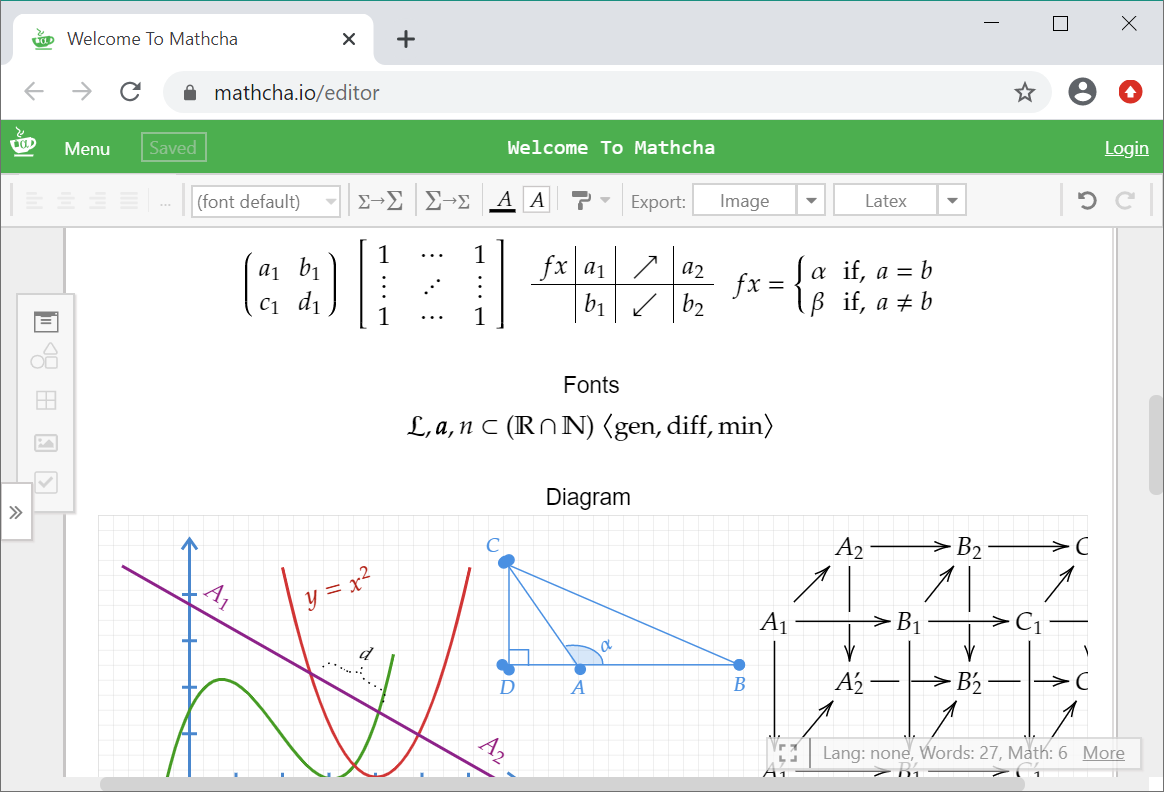
Этот редактор — визуальный: вы сразу редактируете документ вместе с форматированием. В отличие от моего редактора Upmath, в котором вы редактируете исходник на маркдауне и латехе, хотя и сразу видите результат.
Вот рисунок, который я сделал с помощью Mathcha. Накидал основу в нем, экспортировал в TikZ и подправил исходный код уже в UpMath.
$$ \tikzset{every picture/.style={line width=0.75pt}} %set default line width to 0.75pt \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1] %uncomment if require: \path (0,300); %set diagram left start at 0, and has height of 300 %Shape: Boxed Line [id:dp7642567693966007] \draw (130,80) -- (130,140) ; %Shape: Boxed Line [id:dp02318954146147889] \draw (130,150) -- (130,180) ; %Shape: Boxed Line [id:dp4638027067588357] \draw (130,190) -- (130,250) ; %Shape: Wave [id:dp03622557580885122] \draw [color={rgb, 255:red, 74; green, 144; blue, 226 } ,draw opacity=1 ] (215,80) .. controls (202.19,83.1) and (190,86.06) .. (190,89.5) .. controls (190,92.94) and (202.19,95.9) .. (215,99) .. controls (227.81,102.1) and (240,105.06) .. (240,108.5) .. controls (240,111.94) and (227.81,114.9) .. (215,118) .. controls (202.19,121.1) and (190,124.06) .. (190,127.5) .. controls (190,130.94) and (202.19,133.9) .. (215,137) .. controls (227.81,140.1) and (240,143.06) .. (240,146.5) .. controls (240,149.94) and (227.81,152.9) .. (215,156) .. controls (202.19,159.1) and (190,162.06) .. (190,165.5) .. controls (190,168.94) and (202.19,171.9) .. (215,175) .. controls (227.81,178.1) and (240,181.06) .. (240,184.5) .. controls (240,187.94) and (227.81,190.9) .. (215,194) .. controls (202.19,197.1) and (190,200.06) .. (190,203.5) .. controls (190,206.94) and (202.19,209.9) .. (215,213) .. controls (227.81,216.1) and (240,219.06) .. (240,222.5) .. controls (240,225.94) and (227.81,228.9) .. (215,232) .. controls (202.19,235.1) and (190,238.06) .. (190,241.5) .. controls (190,244.57) and (199.7,247.26) .. (210.89,250) ; %Straight Lines [id:da008457960885399407] \draw (190,80) -- (190,250) ; %Flowchart: Summing Junction [id:dp09695643217509597] \draw (135,132.75) .. controls (135,128.75) and (138.36,125.5) .. (142.5,125.5) .. controls (146.64,125.5) and (150,128.75) .. (150,132.75) .. controls (150,136.75) and (146.64,140) .. (142.5,140) .. controls (138.36,140) and (135,136.75) .. (135,132.75) -- cycle ; \draw (137.2,127.62) -- (147.8,137.88) ; \draw (147.8,127.62) -- (137.2,137.88) ; %Shape: Inductor [id:dp3454355331692156] \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; %Straight Lines [id:da4690178114375858] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,185) -- (190,165) ; %Straight Lines [id:da10916309009890135] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,145) -- (190,165) ; % Text Node \draw (112,127) node [anchor=north west][inner sep=0.75pt] [align=left] {A}; % Text Node \draw (112,191) node [anchor=north west][inner sep=0.75pt] [align=left] {B}; \end{tikzpicture} $$
Кеширование в nginx
В прошлый раз мы рассмотрели, как в теории работает кеш и какие ошибки обычно совершают при его программировании. В этот раз я расскажу, как с помощью нескольких настроек nginx включить кеширование прямо на уровне
Я уже писал о том, как работает мой сервис генерации картинок с формулами на латехе. При первом обращении к
Иногда папку с кешем приходится удалять, если она слишком сильно разрослась. Или если я вношу правки в систему, и кеш устаревает. Посетители популярных страниц генерируют множество запросов к одинаковым формулам. В кеше их нет. Nginx направляет запросы к PHP. PHP на каждую формулу вызывает консольный скрипт латеха. Раньше у меня не было защиты от того, чтобы сервер в нагруженном состоянии хотя бы не делал одно и то же много раз. Это классическое условие гонки.
Как оказалось, приемлемое решение — включить кеш в nginx и настроить блокировку. Тогда он пропускает на бэкенд разные запросы, а одинаковые выстраивает в очередь ожидания. Результат записывает в свой внутренний временный кеш и отдает всем ожидавшим клиентам.
В блоке конфигурации http указываем папку и другие параметры зоны кеша:
fastcgi_cache_path /var/data/i.upmath.me levels=1:2 keys_zone=i_upmath:10m;
fastcgi_cache_key "$scheme$request_method$host$request_uri";Обратите внимание на ключ кеширования. Я использовал обычный адрес ресурса, потому что картинки публичны и одинаковы для всех. Если у вас закрытые ресурсы, можете попробовать добавить куки в ключ. Хотя я бы не стал так делать: велик риск ошибки и утечки чужих приватных данных через кеш.
Далее в нужном location подключаем зону:
fastcgi_cache i_upmath;
fastcgi_cache_valid 200 10m;
fastcgi_cache_methods GET HEAD;
fastcgi_cache_lock on;
fastcgi_cache_lock_age 9s;
fastcgi_cache_lock_timeout 9s;Помимо кеширования здесь включена блокировка для предотвращения race condition. Длительность блокировки и ожидания я выбрал 9 секунд, потому что таймаут запуска латеха в моей системе 8 секунд. Вы можете подобрать другое значение.
На моем сервере ограниченное количество процессов
fastcgi_buffers 8 16k;
fastcgi_buffer_size 32k;
fastcgi_connect_timeout 90;
fastcgi_send_timeout 90;Технически правильное решение в моей ситуации — прогревать новый кеш, пока система работает со старым. А именно, брать часть текущего потока запросов формул, генерировать для них новые картинки и складывать в новую папку. Когда популярные формулы окажутся в новом кеше, переключать папки.
С прогревом нового кеша пользователи не заметят подмены, и сервер будет работать в комфортном режиме. Но систему прогрева нужно еще программировать. А решение с nginx внедряется простой правкой конфига. Конечно, картинки с формулами у некоторых пользователей в момент очистки кеша перестают открываться. Но для
Стили для печати и конвертация в PDF
Постоянные читатели помнят, что у меня есть двухпанельный редактор математических текстов Upmath: слева пишете текст с разметкой на маркдауне и латехе, справа получаете результат.
От пользователя пришло письмо, в котором он спрашивает, есть ли конвертация маркдауна и латеха в PDF. Вопрос задают не первый раз. Мне сообщали о
Главная задача сервиса Upmath — подготовка математических текстов для публикации в вебе. Результат его работы —
Но сейчас я задумался. Не всем нужен высококачественный PDF.
Печатать можно напрямую из браузера. Хоть на настоящем принтере, хоть в
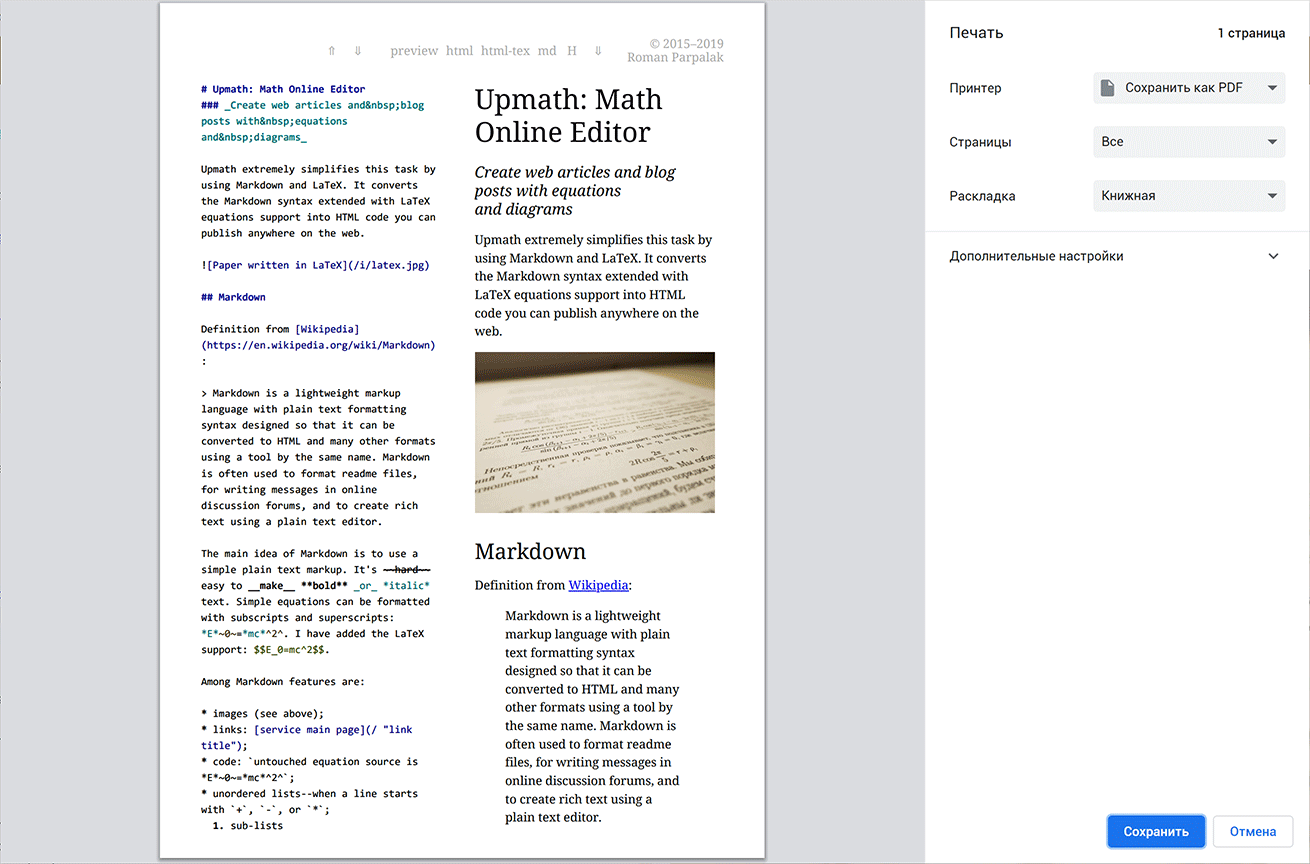
Мне ничего не стоило добавить стили для печати. Результат сразу преобразился:
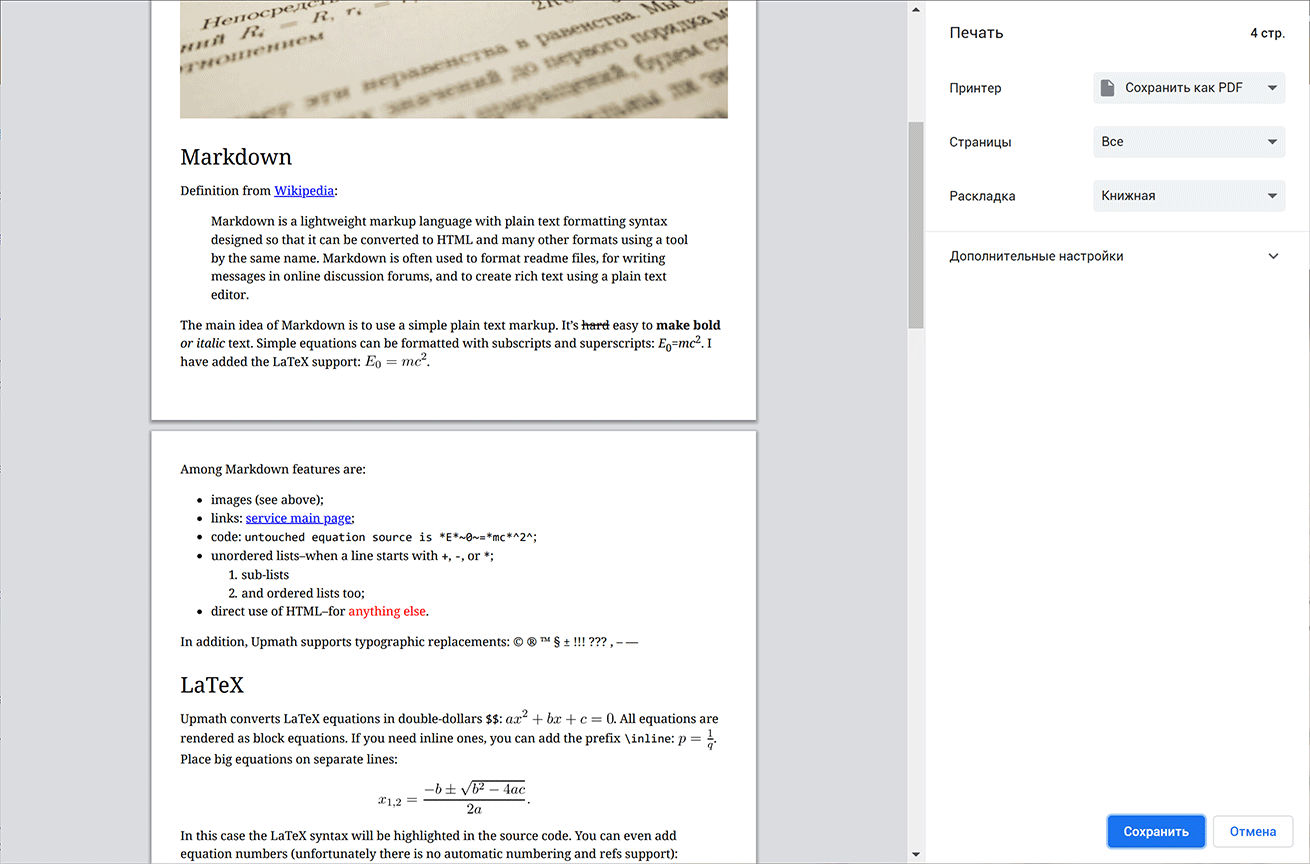
Качество получающихся документов мне не очень нравится. Я добился того, чтобы картинки не разбивались на две страницы. Но исключить разрыв страницы после заголовков у меня не получилось. Не понимаю, почему ни хром, ни FF не понимают инструкцию
h1, h2, h3 {
break-after: avoid;
}Будем ждать, пока эти баги в браузерах будут исправлены.
О схеме URL сервиса генерации картинок с формулами
В посте про объемный чертеж я привел саму картинку, но не ее код. А без кода картинка бесполезна: нельзя ни подсмотреть, как она сделана, ни изменить под свои нужды.
На самом деле код картинки содержится в ее адресе. Как писал Якоб Нильсен 19 лет назад, URL — это интерфейс. И я принял такое интерфейсное решение. Формула на латехе (например, a^2+b^2=c^2) кодируется и добавляется в урл:
//i.upmath.me/svg/a%5E2%2Bb%5E2%3Dc%5E2По нему открывается сама картинка с формулой: $$a^2+b^2=c^2$$.
Таким образом, из адреса картинки расшифровкой можно получить ее исходный код. Чтобы облегчить этот процесс, я сделал адрес другого вида (от svg остается последний символ):
//i.upmath.me/g/a%5E2%2Bb%5E2%3Dc%5E2По этой ссылке открывается
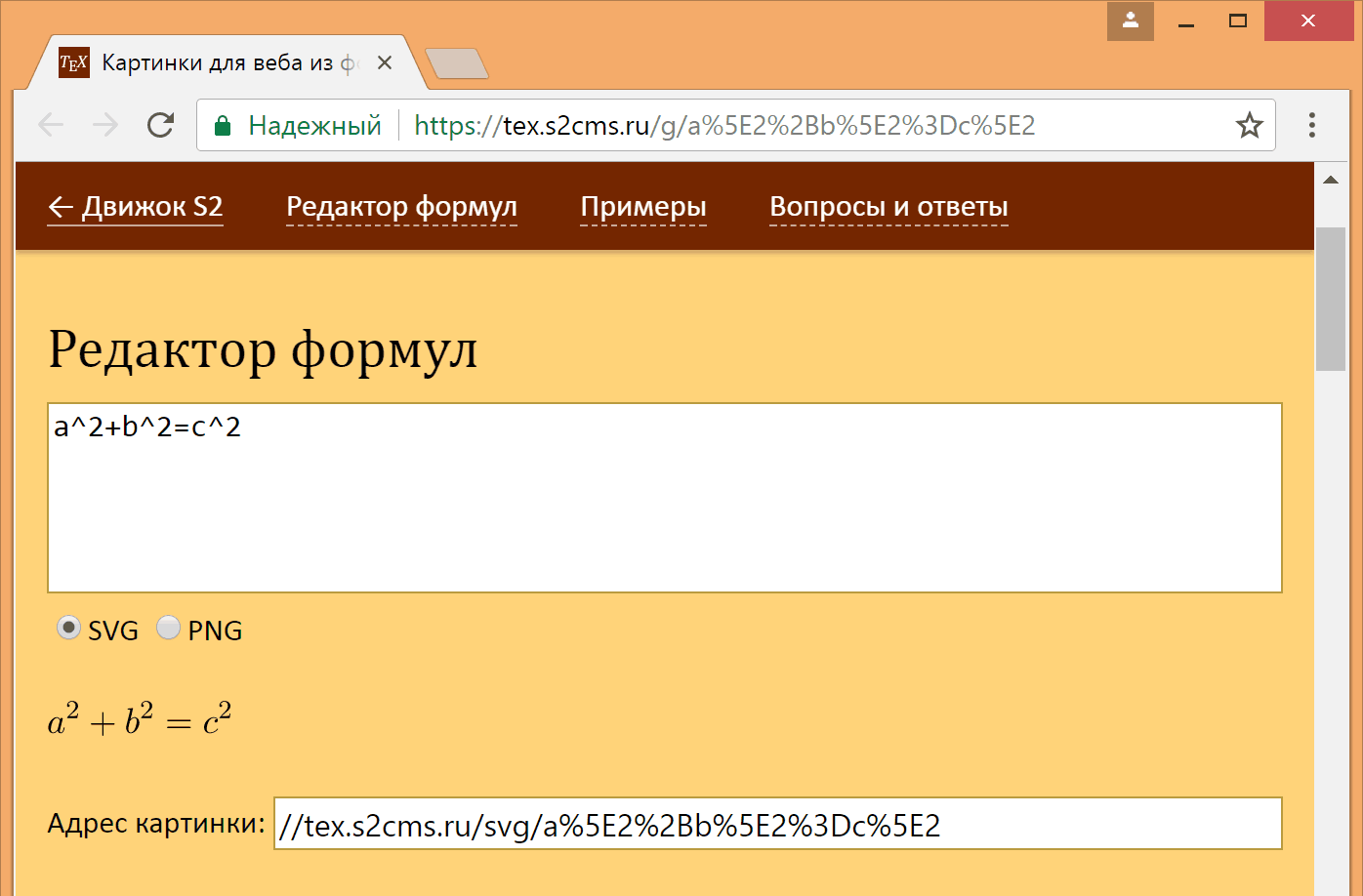
Вообще, исходный код может быть достаточно длинным. Вот пример, в котором на комплексной плоскости отмечены первые 10 степеней числа $$1+i\pi/10$$:
\begin{tikzpicture}[scale=1.0545]\small
\tikzset{>=stealth}
\def\k{10}
\def\p{3.1415926/\k}
\def\r{3.1}
\def\l{5.8}
\def\t{0.07}
\draw[->,thin,gray] (-\l,0)--(\l,0);
\draw[->,thin,gray] (0,-0.6)--(0,\l);
\draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$};
\foreach \l in {1,...,\k}
\draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)});
\draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$};
\draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$}
(-\r,\t)--(-\r,-\t) node[below]{$-1$}
(\t,\r)--(-\t,\r) node[left]{$1$}
(0,0) node [anchor=north west,yshift=-0.07cm] {$0$};
\draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l);
\end{tikzpicture}Результат:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{10} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$}; \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Этот пример я взял из статьи о формуле Эйлера $$e^{i\pi}=-1$$. Первую версию картинки рисовал вручную. В Maple выполнил возведение в степень и построил график. Открыл его в фотошопе и поверх дорисовал
На версию с графиком в tikz ушло столько же времени, или даже больше. Но масштабируемость результата находится на совершенно другом уровне. Чтобы нарисовать первым способом вдвое больше векторов, нужно потратить вдвое больше времени. Второй способ требует изменения одного числа k в исходном коде, и foreach сделает всю работу. Вот 20 векторов:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{20} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Вот 50:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{50} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
URL последней картинки длиной 1192 символа. В принципе, такие длинные адреса не очень красивы. Но и большой проблемы в этом нет. В стандарте нет ограничений на длину URL, да и с практическим ограничением в браузере или
Меня просили изменить алгоритм кодирования, чтобы укоротить адреса.
Необходимости в этом я пока не вижу. Но если буду делать доработку, то поступлю аналогично. Адрес /svgb/... с закодированными в /gb/... на дешифрованный вариант в редакторе формул.
Объемный чертеж
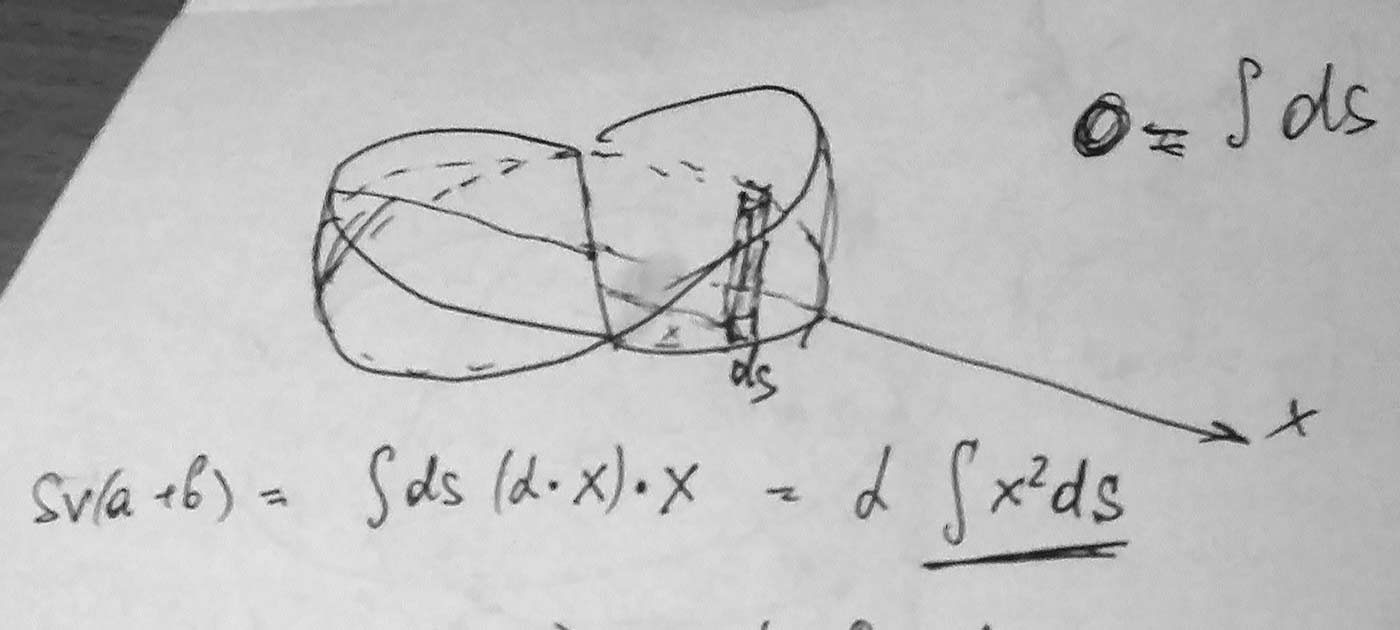
Нарисовал в латехе объемный чертеж, но он не пригодился. Так что просто оставлю его здесь.
Чтобы делать такие чертежи, добавил в свой редактор математических текстов Upmath поддержку пакета
Сравните с версий того же чертежа из черновика:
Синхронная прокрутка
Этот текст я написал в том числе и для себя, чтобы в следующий раз не попадать в ловушку «почему два года назад я сделал так криво, сейчас всё исправлю».
Иногда в интерфейсе нужно одновременно показать два документа с синхронной прокруткой. Прокручиваешь левый документ, и правый тоже прокручивается до соответствующего места. И наоборот. Может показаться, что задача синхронной прокрутки не слишком сложная. Но на самом деле это не так.
Пример синхронной прокрутки есть в каждом интерфейсе просмотра изменений файлов. Вот PhpStorm:
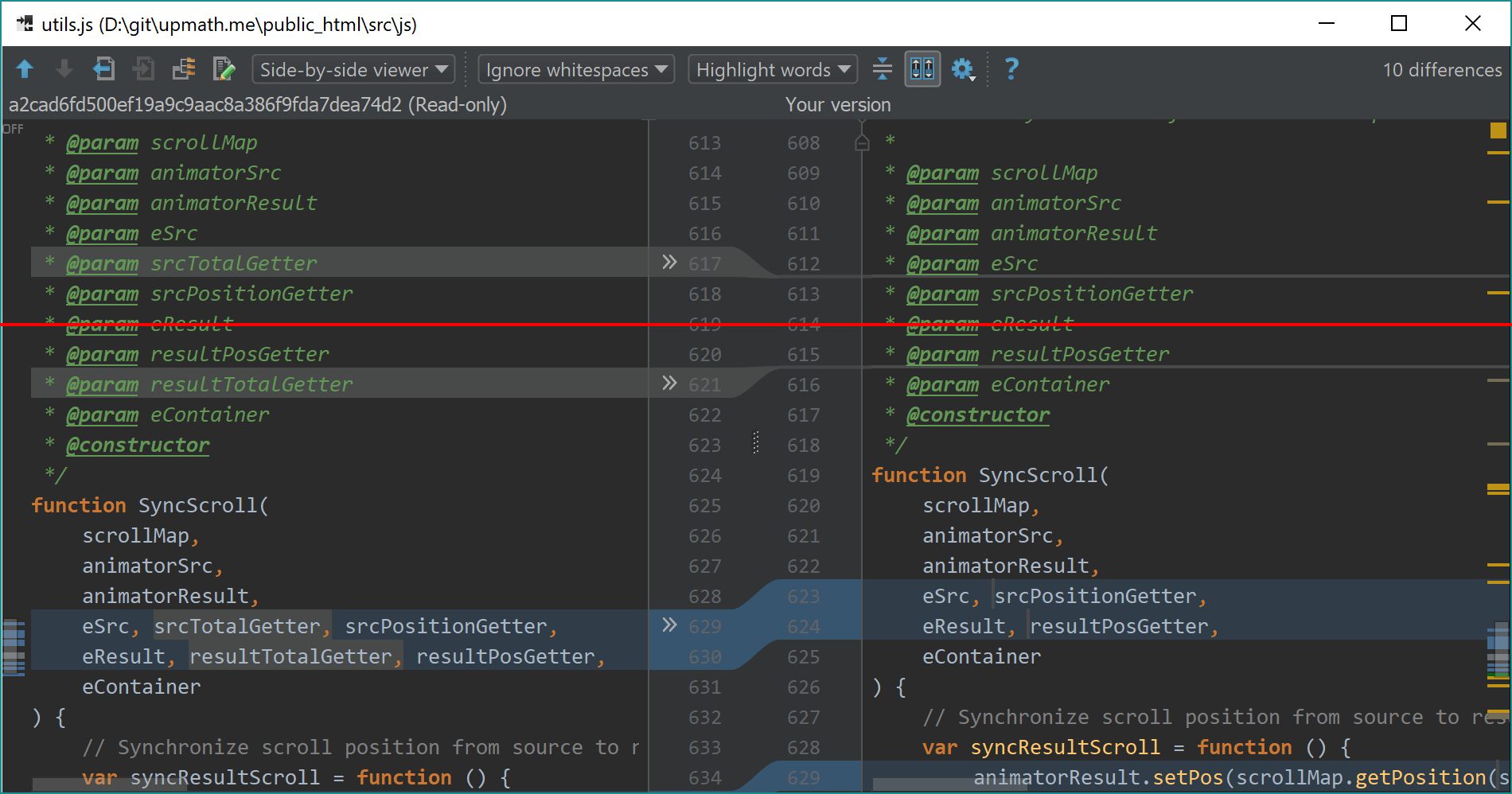
При прокрутке одной версии документа вторая всегда выравнивается так, чтобы на красной линии оказались соответствующие строки. Аналогичный способ я выбрал для своего редактора математических текстов, только ориентир выравнивания сделал посередине:
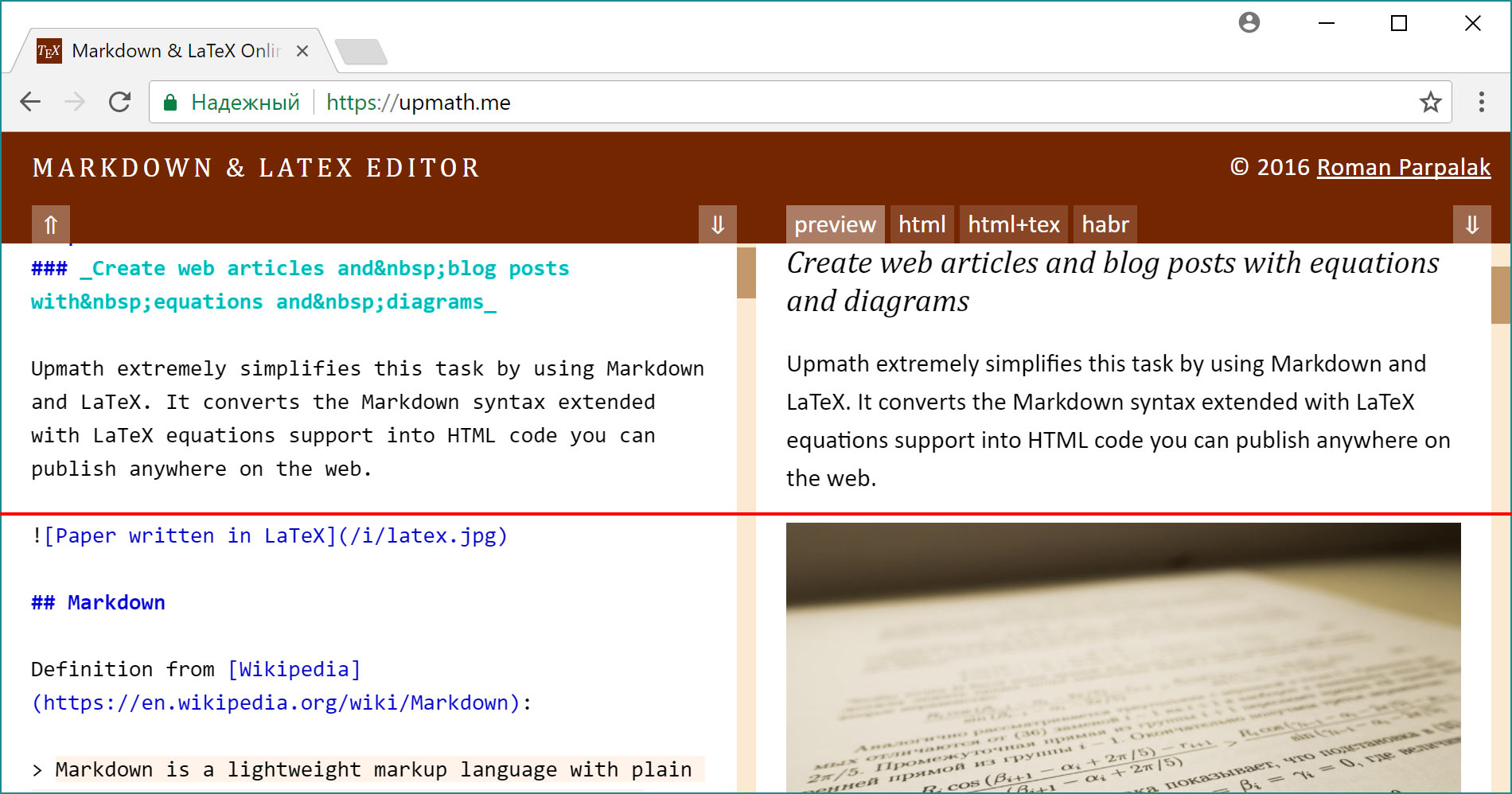
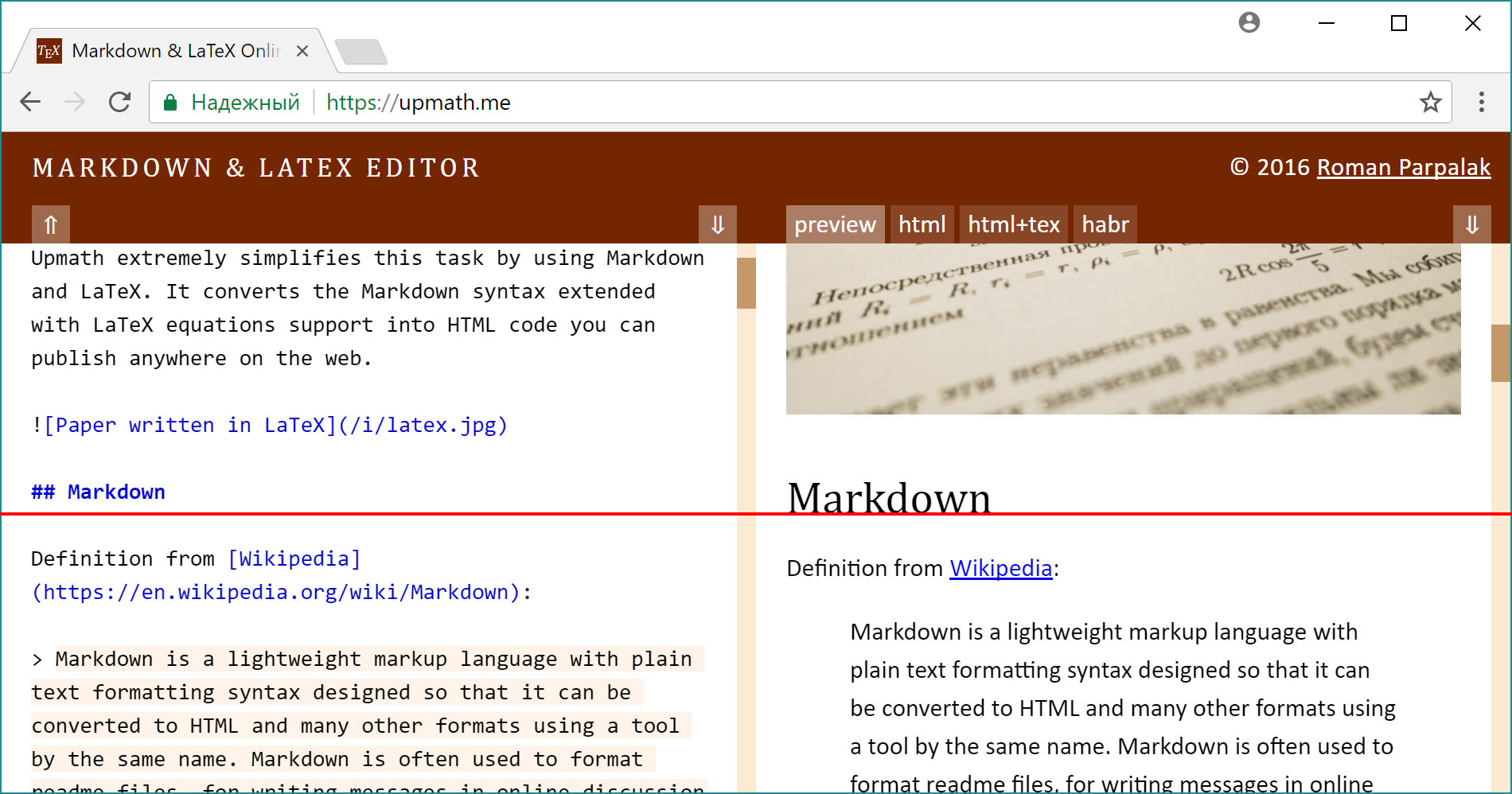
Здесь мы набираем исходный код и сразу же видим результат. Обратите внимание на неравномерность прокрутки. Слева картинка кодируется одной строкой, а справа она занимает почти всю высоту прокручиваемой области.
Такая неравномерность приводит к ряду проблем. Когда картинка добавляется последней строчкой, в предпросмотре отображается только ее верхушка:
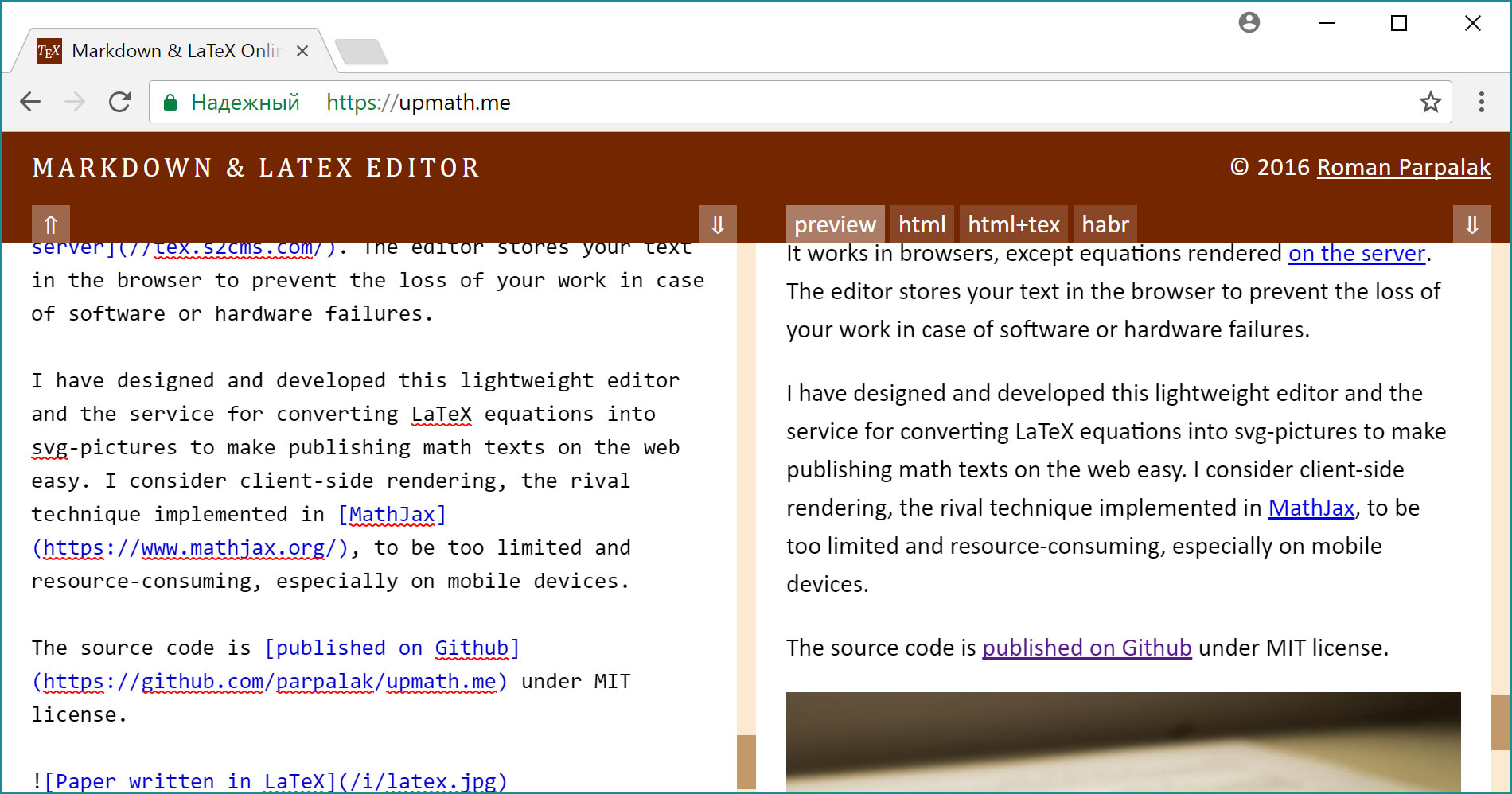
Это естественное поведение алгоритма с выравниванием по ориентиру в центре. И его хотелось бы улучшить. Но от
Другая идея — сделать ориентир не фиксированным, а подвижным. Сначала ориентир расположен вверху. Затем, по мере прокрутки, он сдвигается вниз. Но и здесь нас ждут скользкие моменты. Например, мы знаем, что начало одного и того же абзаца находится в левом документе на высоте в 30%, а в правом на 50%. Пусть левый документ прокрутили на 30%. Тогда мы говорим, что ориентир тоже находится на 30% высоты экрана, переводим 30% в 50%, и располагаем правый документ так, чтобы абзац был на 30% высоты экрана. Проблема в том, что обратное преобразование не обязано давать тот же самый результат. Действительно, тот же самый абзац будет использоваться при прокрутке правого документа на 50%, и в общем случае это разные положения прокрутки. В такой реализации встречаются странные скачки прокрутки при переключении фокуса между документами и даже немонотонность зависимой прокрутки: если вы прокручиваете один документ вниз, то другой в некоторые моменты будет двигаться не вниз, а вверх.
У меня была мысль отказаться от двух прокручиваемых областей, прокручивать только исходный код и умным алгоритмом выводить в области предпросмотра соответствующую область документа. Но проблемы синхронной прокрутки, о которых я рассказал, мешают это сделать.

Похоже, полностью избавиться от проблем синхронной прокрутки вообще нельзя. Вернемся к сравнению файлов. Предположим, в одном файле 100 строк, во втором я превратил сотую строку в еще 400. Прокручивая первый файл, мы никогда не увидим новые 400 строк второго. Как бы мы ни выравнивали второй файл, все 400 строк на экран не поместятся. Это значит, что нельзя убирать вторую прокрутку.
В своем редакторе я оставил синхронизацию прокрутки по ориентиру, но дополнил ее условием: если один документ полностью прокручен вверх или вниз, то второй документ прокручивается полностью.
Формулы
Открываем 10 лучших публикаций на хабре за неделю и видим, что на четвертом месте статья «Сказ царя Салтана о потенциале лапласиана», на пятом — «Байесовская нейронная сеть — теперь апельсиновая (часть 2)». И обе с использованием моего сервиса для формул.
Неплохо, я считаю :)
См. Markdown and LaTeX online editor и описание на хабре.
Латех в вебе
Постоянные читатели помнят, что у меня есть движок сайтов S2, и он с помощью расширения s2_latex ищет в тексте страницы формулы на латехе и заменяет их на картинки. Расширение обращается к сервису codecogs.com. Этот сервис зачастую глючит, и я уже давно сделал свой, с
Мой сервис делает из формул картинки. Вот, для примера, знакомое всем решение квадратного уравнения в SVG и PNG:
На обычных мониторах преимуществ у SVG нет. Но на ретине или при большом увеличении SVG выглядит более чем достойно. А за ретиной будущее.
В

Символы в формулах крупнее и жирнее, чем в окружающем тексте. Они в буквальном смысле выпадают из окружающего текста. Меняем гротеск на антикву, увеличиваем кегль и добавляем выравнивание по базовой линии:

Теперь буквы в формулах аккуратно располагаются на тех же линиях, что и буквы в окружающем тексте. Чтобы заработала магия с выравниванием по базовой линии, к странице нужно подключить специальный скрипт.
У
Я подготовил описание сервиса и инструкцию. Посмотреть сервис в работе можно в блоге о теоретической физике. В следующий раз я расскажу о том, как всё это работает.